기획자와 개발자들은 협업하며 종종 부딪힌다.
정리되지 않은 수많은 아이디어들을 한아름 들고 오는 기획자.
이것도 안되고, 저것도 안된다고 하는 개발자.
둘은 오늘도 서로에게 고개를 저으며 한숨을 내쉰다.
이런 세상의 수많은 기획자와 개발자들 사이 갈등 속 각자 나름의 사정은 천차만별이지만, 근본적인 원인은 크게 다르지 않다.
바로 ‘서로가 서로의 일을 모른다’는 것
우리들은 서로의 일을 조금이나마 이해해 보려 노력할 필요가 있다.
서로를 이해하고 상대방이 바라보는 곳을 함께 바라볼 수 있어야 발전적인 대화가 가능하다.
별 헤는 밤을 기획하면서 나 역시도 개발자들과 수없이 부딪히곤 했고, 다양한 방식으로 문제를 해결해 나가려 노력했다.
이 글에서는 별 헤는 밤 프로젝트를 진행하며 생겼던 사례들을 살펴보며, 초보 기획자의 입장에서 우리의 개발자들을 이해하는 시간을 가져보고자 한다.
성능을 향상시키기
우리는 앞선 시간에서, 데이터베이스의 index라는 자료구조를 중심으로 데이터를 어떻게 정리하는 것이 효율적인가에 대해 고민해보았다.
[개발자와 화해하기] 데이터를 정리하는 법 : index 이해하기 (1)
기획자와 개발자들은 협업하며 종종 부딪힌다. 정리되지 않은 수많은 아이디어들을 한아름 들고 오는 기획자. 이것도 안되고, 저것도 안된다고 하는 개발자. 둘은 오늘도 서로에게 고개를 저으
starsufers.tistory.com
여기서는 데이터의 정리 방식에 따라 시간복잡도가 변화하기 때문에 index를 사용할 경우, 수직적인 데이터 정리 방식이 효율적일 수 있음을 언급했다. 그렇다면 왜 index에서 수직적인 데이터 정리 방식이 index의 성능 향상에 도움을 주는가? 그 답은 B-Tree라는 자료구조에 있다.
B-Tree(B-트리)
B-Tree는 데이터베이스와 파일 시스템에서 보편적으로 사용되는 자료구조의 일종으로, 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조를 말한다.
이런 구조는 왜 필요할까? 방대한 양의 자료를 검색할 때, 검색어와 자료를 하나하나 비교하는 방식은 비효율적이다. '업 앤 다운' 게임을 예로 들어보자. 1~100 까지의 무작위 숫자 하나를 맞추는 게임을 할 때, 어떤 조건 없이 단순히 그 수를 찾기 위해서는 1부터 100까지 최대 100번을 질문해야 한다. 이는 누가 봐도 비효율적이다. 그래서 이 게임에서는 말한 숫자보다 정답이 더 큰(작은) 수 인지 알려준다. 이 경우 가장 빠르게 정답에 도달할 수 있는 방법은 무엇일까?
모두 알고 있듯 주어진 범위에서 중간값만을 부르는 전략을 반복하면 된다.
위 예시의 다음과 같은 3가지 케이스를 살펴보자.
| 정답 | 88 | 23 | 55 | 1 | 100 |
| 시행 | 1) 51 --- Up 2) 76 --- Up 3) 89 --- Down 4) 83 --- Up 5) 86 --- Up 6) 87 --- Up |
1) 51 --- Down 2) 25 --- Down 3) 13 --- Up 4) 19 --- Up 5) 22 --- Up 6) 23 |
1) 51 --- Up 2) 76 --- Down 3) 58 --- Down 4) 55 |
1) 51 --- Down 2) 25 --- Down 3) 13 --- Down 4) 7 --- Down 5) 4 --- Down 6) 2 --- Down |
1) 51 --- Up 2) 76 --- Up 3) 89 --- Up 4) 95 --- Up 5) 98 --- Up 6) 100 |
이 전략을 사용할 경우 log2(100) = 6.6438... 이므로 어떤 수가 나오더라도 최대 7회 안에 무조건 정답을 맞출 수 있다. 데이터베이스에서 내가 원하는 자료를 효율적으로 찾는 과정도 이와 매우 유사하다. 우리가 수많은 아이디어를 우후죽순처럼 던질 동안, 개발자들은 이를 구현하기 위해 배 이상의 수많은 방식을 고민했다. 이진 탐색 트리(Binary Search Tree)를 보면 위와 굉장히 유사한 방식으로 원하는 데이터를 찾아나감을 알 수 있다. 이 경우 트리의 높이를 h라 할 때 O(h)의 시간복잡도를 갖는다고 하는데, 이는 검색에서 굉장히 중요한 용어이니 잘 기억하고 있도록 하자. 이진 탐색 트리에 대해 자세히 알아보고 싶다면 다음 자료를 참고할 수 있다.
[자료구조] 이진탐색트리(Binary Search Tree)의 개념, 이해 | C언어 이진탐색트리 구현
이진탐색트리(Binary Search Tree)이란? 이진탐색트리란 다음과 같은 특징을 갖는 이진트리를 말한다. ( #이진트리 - 각 노드의 자식 노드가 최대 2개인 트리) 1. 각 노드에 중복되지 않는 키(key)가 있다
code-lab1.tistory.com
B-Tree 역시 방대한 규모의 자료 속에서 원하는 데이터에 최적의 방식으로 접근하기 위해 고안된 구조이다.

B-Tree는 위와 같은 구조를 가진다. 맨 위 (7,20)이 표시되어 있는 노드(특정한 지점을 일컫는 말)를 루트 노드(Root Node), 중간에 있는 노드들을 자식 노드(Child Node), 종단에 있는 노드들을 리프 노드(Leaf Node)라고 부른다. 내부에 있는 숫자들은 키(Key)라고 부르며, M = n 일 경우 최대 n개의 자식을 가질 수 있는 n차 B트리라고 부른다.
원하는 데이터가 22 일 때, 탐색은 다음의 과정을 거친다.

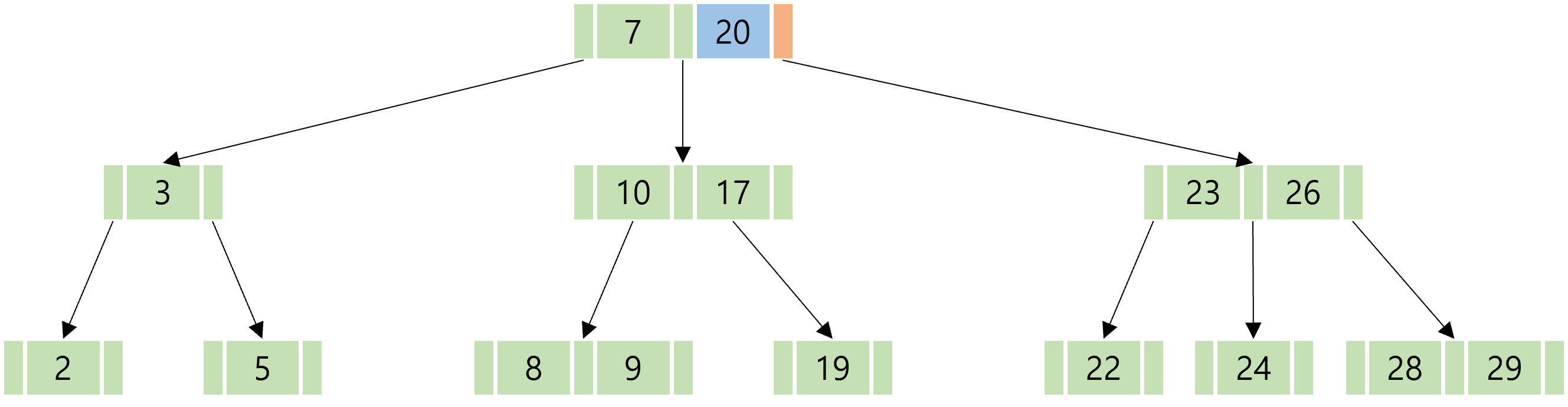
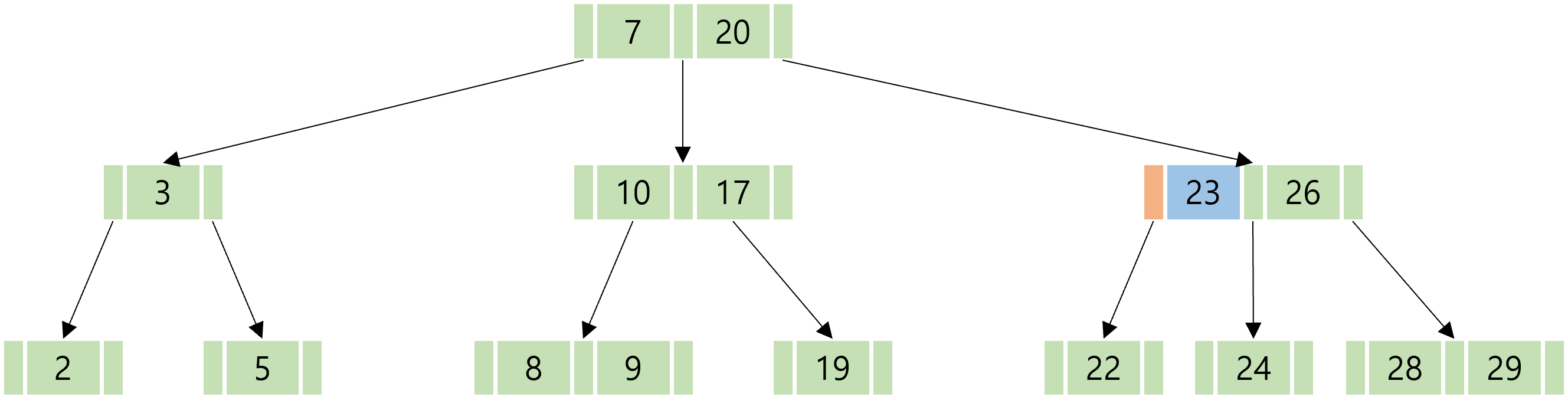
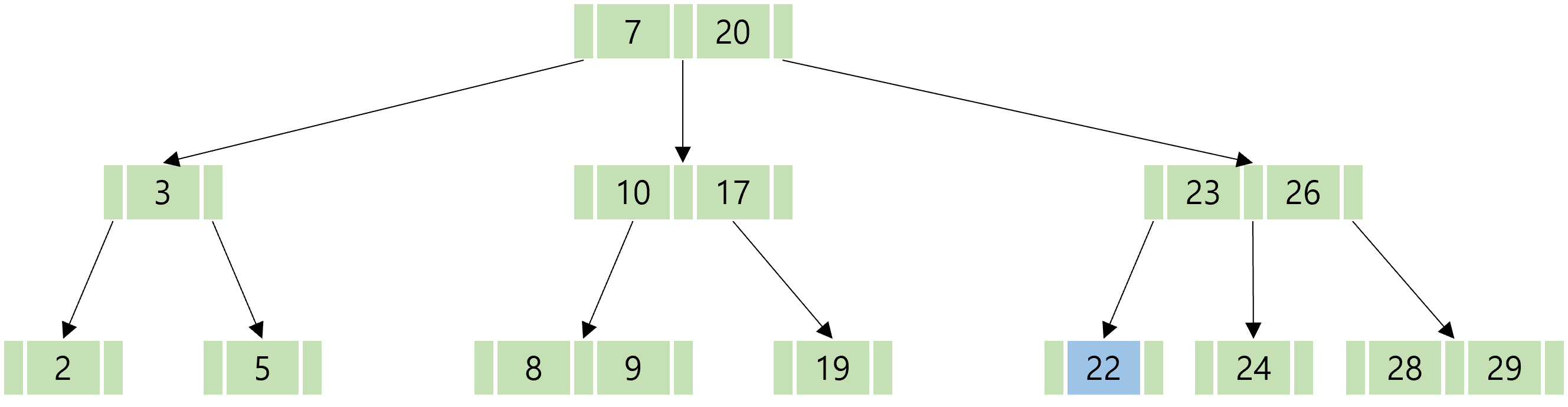
B-Tree의 경우에도 마찬가지로 O(h)의 시간복잡도를 갖는다. 그러나 주요한 차이는 이전의 방식에 비해 포인터 접근 수를 최소화하여 더 큰 규모에서 더 빠른 탐색 시간을 보장한다는 데에 있다. 데이터의 규모가 방대할 수록, 더욱 효율적인 탐색 방식이 필요하다. B-Tree에는 이외에도 삽입, 삭제, 분할 등의 과정이 있지만 우리는 대강 이런 구조로 이루어져 있다는 것만 일단 알아가도록 하자. 더 자세히 알고 싶다면 아래 글에 자세히 설명되어 있으니 참고해도 좋다.
[자료구조] 그림으로 알아보는 B-Tree
B트리는 이진트리에서 발전되어 모든 리프노드들이 같은 레벨을 가질 수 있도록 자동으로 벨런스를 맞추는 트리입니다.
velog.io
빠른 검색을 위해서
어느 기획자나 내가 만든 서비스 내부의 검색 기능이 멋지고, 빠르고, 효과적으로 작동하기를 원한다. 로딩이 무한으로 돌아가는 상황을 그 누구도 바라지 않는다. 심지어 5초. 아니 3초만 넘어가도 갑갑해하는 경우가 대다수다. 내가 소비자여도 그러할 것이다. 그러나 이를 개선하기 위해 데이터를 효과적으로 분류하고, 정리하고, 더 좋은 방법을 고안할 수 있는 기획자는 많지 않다.
지난 시간이 개발자의 요청의 원인을 이해하는 단계였다면, 이번 시간은 그 원인을 조금이나마 더 깊게 파고들어보는 시간이라 요약할 수 있겠다. 데이터를 많이 다루게 될 기획자라면, 이와 같은 자료구조에 대해서도 공부해야 할 필요가 있을 것이다.
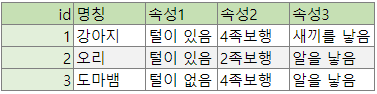
이론적 접근에 다소 따분함을 느꼈을 독자들을 위해 다음 시간에는 실제로 '예시 1'의 데이터를 완벽하게 '예시 2'와 같이 변경하는 방법에 대해 실무적 접근을 해보고자 한다.
<별 헤는 밤> 구경하기 👀
별 헤는 밤: 밤하늘, 별자리, 여행정보와 날씨예보까지 - Google Play 앱
오늘부터 별잘알! 오늘밤 별자리 정보, 날씨·광공해·월령까지 고려한 '관측적합도', 주변 관측지 검색으로 누구나 쉽게 밤하늘을 즐겨보세요.
play.google.com
'별밤 일지 > 기획' 카테고리의 다른 글
| [개발자와 화해하기] 데이터를 정리하는 법 (3) : 간단한 가로/세로 데이터 변환 (1) | 2024.01.09 |
|---|---|
| [티스토리 블로그 만들기] 북클럽 스킨 정사각형 프로필 설정 방법과 크기, 위치 변경하기 (0) | 2023.12.28 |
| [티스토리 블로그 만들기] 홈프로모션 설정하기!라고 적고 티스토리 망치는 방법이라고 읽는다! (0) | 2023.11.14 |
| [개발자와 화해하기] 데이터를 정리하는 법 (1) : index 이해하기 (0) | 2023.10.13 |
| [티스토리 블로그 만들기] 티스토리에서 살아남기 그 1장 (0) | 2023.09.05 |



